接下来将介绍组合优化和更普遍的线性规划中的算法工具，这些工具可用于以数值方式求解最优传输（离散）。

0. Graph theory

在阅读过程中，会涉及到图论的一些内容，这里简要记录下，便于后续理解。
可以参考图论学习笔记，我尽量将涉及到的概念定理进行补充。

• 完全图：满足任意两个不同的节点都由一条边相连的简单图。对于包含 n 个节点的图，只有一个完全图，表示为 $K_n$
  
  
• 二分图（bipartite graph):节点集合 V 可以写成2个完全不相交的子集 A、B的并集，且对于在同一子集的任意一对节点，都不存在连接这对节点的边。记为$G=(A,B,E)$。
  
  
• 完全二分图（complete bipartite graph）：集合A、B中的任意两点都有边连接。
  
  
• 链(walk)： $W$是$G$节点和边构成的一个序列$(v_0,e_1,v_1,\ldots,e_k,v_k)$ ,边$e_i$有端点
  $v_{i-1},v_i$ 。$v_0$ 为开始节点，$v_k$ 为结束节点。用 uv− walk表示一个开始节点为 u ，结束节点为 v 的链
• 路径（path）：为一个没有重复边和节点的链
• 环 (cycle)：为一个没有重复边和节点的链$(v_0,e_1,v_1,\ldots,e_k,v_k)$ ,除了第一个和最后一个
  节点相同，即$v_0=v_k$。
• 连通（connected）：图G是连通的，若 G 中任意两个节点都可以被一份路径相连，即总能找到一个uv-path。
• 森林（forest）：是一个无环图（acyclic graph）
• 树（tree）：是一个连通无环图（connected acyclic graph）
• 叶（leaf）：是一个图中度为 1 的节点

Tree Theorem
每个有 n 个节点的树都有正好 n−1 条边

• 如果图是 树，那么它是一个连通的无环图，其边数总是等于节点数减一，即：
  $E=N−1$
• 如果图是 森林（一个由多个不连通的树组成的图），那么边数与节点数的关系是：
  $E=N−C$
  森林中每个树的边数都是少于节点数的。

1. The Kantorovich Linear Programs

回忆Kantorovich’s optimal transport problem：

$$
\mathcal{L}_{{\mathbf{C}}}(\mathbf{a},\mathbf{b})\stackrel{\mathrm{def.}}{=}\min_{{\mathbf{P}\in\mathbf{U}(\mathbf{a},\mathbf{b})}}\langle\mathbf{C},\mathbf{P}\rangle\stackrel{\mathrm{def.}}{=}\sum_{i,j}\mathbf{C}_{i,j}\mathbf{P}_{i,j}.
$$

转化为标准线性规划形式：

$$
\mathcal{L}_{\mathbf{C}}(\mathbf{a}, \mathbf{b}) =
\min_{\substack{\mathbf{p} \in \mathbb{R}_+^{nm} \\ A\mathbf{p} = \begin{bmatrix}\mathbf{a} \\ \mathbf{b}\end{bmatrix}}}
\mathbf{c}^\mathrm{T} \mathbf{p}.
$$

其中 $c、p$ 为矩阵 $C、P$ 每列元素依次堆叠而成,而A为满足$P \in U(a,b)$的约束矩阵：

$$
A=\begin{bmatrix}\mathbb{1}_n^{\mathrm{T}}\otimes\mathbb{I}_m\\\mathbb{I}_n\otimes\mathbb{1}_m^{\mathrm{T}}\end{bmatrix}\in\mathbb{R}^{(n+m)\times nm}
$$

注意到：$$A \begin{bmatrix} \mathbf{1}_n \\ \mathbf{0}_m \end{bmatrix} = A \begin{bmatrix} \mathbf{0}_n \\ \mathbf{1}_m \end{bmatrix} = \mathbf{1}_{nm}^\mathrm{T}$$
矩阵A的行向量线性相关，因此 A定义的n+m个线性约束中，至少有一个约束是冗余的。为了避免处理 a和 b 时出现不对称的情况，选择保留冗余的约束形式,但需注意的是由于矩阵A的退化，在随后的计算中可能会出现问题。
上述线性规划问题由对偶理论可得出其对偶形式：

$$
\mathcal{L}_\mathbf{C}(\mathbf{a},\mathbf{b})=\max_{\begin{array}{c}\mathbf{h}\in\mathbb{R}^{n+m}\\A^\mathrm{T}\mathbf{h}\leq\mathbf{c}\end{array}}\left[\begin{array}{c}\mathbf{a}\\\mathbf{b}\end{array}\right]^\mathrm{T}\mathbf{h}
$$

（简要推导见附录）

2.C-transforms

回忆在之前曾给出Kantorovich作为一个约束凸最小化问题对应的对偶问题：

$$
\mathcal{L}_\mathbf{C}(\mathbf{a},\mathbf{b})=\max_{(\mathbf{f},\mathbf{g})\in\mathbf{R}(\mathbf{a},\mathbf{b})}\langle\mathbf{f},\mathbf{a}\rangle+\langle\mathbf{g},\mathbf{b}\rangle
$$

其中：

$$
\mathbf{R}(\mathbf{a},\mathbf{b})\overset{\mathrm{def.}}{\operatorname*{=}}\{(\mathbf{f},\mathbf{g})\in\mathbb{R}^n\times\mathbb{R}^m:\forall\left(i,j\right)\in\left[n\right]\times\left[m\right],\mathbf{f}\oplus\mathbf{g}\leq\mathbf{C}\}
$$

考虑任何对偶可行对 $(f , g)$:

• $f^C\in R^m$: C-transform vector of f

$$
(\mathbf{f}^\mathbf{C})_j=\min_{i\in[n]}\mathbf{C}_{ij}-\mathbf{f}_i,
$$

• $g^{\bar{C}}\in R^n$: $\bar{C}$- transform of g

$$
(g^{\bar{\mathbf{C}}})_i=\min_{j\in[m]}\mathbf{C}_{ij}-\mathbf{f}_j
$$

由定义，$(f,f^C) \in R(\mathbf{a},\mathbf{b})$ , $(g^{\bar{C}},g) \in R(\mathbf{a},\mathbf{b})$ ,且满足：

$$
\langle\mathrm{f,~a\rangle+\langle g,~b\rangle\leq\langle f,~a\rangle+\langle f^{C},~b\rangle.}
$$
$$
\langle\mathrm{f,~a\rangle+\langle g,~b\rangle\leq\langle g^{\bar{C}},~a\rangle+\langle g,~b\rangle.}
$$

进一步有：

$$
\langle\mathbf{f},\mathbf{a}\rangle+\langle\mathbf{f}^{\mathbf{C}},\mathbf{b}\rangle\leq\langle\mathbf{f}^{{\mathbf{C}\bar{\mathbf{C}}}},\mathbf{a}\rangle+\langle\mathbf{f}^{\mathbf{C}},\mathbf{b}\rangle\leq\langle\mathbf{f}^{{\mathbf{C}\bar{\mathbf{C}}}},\mathbf{a}\rangle+\langle\mathbf{f}^{{\mathbf{C}\bar{\mathbf{C}}\mathbf{C}}},\mathbf{b}\rangle\leq\ldots
$$

上述不等号并不会一直满足严格不等式关系，具体有以下结论：

$\text{(i) } f \leq f' \Rightarrow f^C \geq f'^C.$
$\text{(ii) } f^{C\bar{C}} \geq f, \quad g^{\bar{C}C} \geq g.$
$\text{(iii) } f^{C\bar{C}C} = f^C.$

(证明见附录)

3.Complementary Slackness

令 $P^*$ and $f^*$, $g^*$ 分别为原始问题与对偶问题最优解。 则有：$$ \mathcal{P}_{i,j^*}(\mathcal{C}_{i,j} - \mathbf{f}_i^- \mathbf{g}_j^T) = 0, \quad (i,j) \in [n] \times [m] $$
即,若$\mathbf{P}_i,j^\star>0$ 则 $\mathbf{f}_i^*+\mathbf{g}_j^*=\mathbf{C}_{i,j};$ 若 $\mathbf{f}_i^*+\mathbf{g}_j^*<\mathbf{C}_{i,j}$ 则 $\mathbf{P}_{i,j}^*=0.$

(Proof)

• 定义：矩阵 $\mathbf{P} \in \mathbb{R}^{n \times m}$ 和向量对 $(\mathbf{f}, \mathbf{g})$ 关于 $\mathbf{C}$ 是互补的，当且仅当对于所有满足 $\mathbf{P}_{i,j} > 0$ 的索引对 $(i, j)$，都有 $\mathbf{C}_{i,j} = \mathbf{f}_i + \mathbf{g}_j$。

如果一对可行的原始变量和对偶变量是互补的，则它们是最优的：

如果 $\mathbf{P}$ 和 $(\mathbf{f}, \mathbf{g})$ 是分别关于 Kantorovich 原问题和对偶问题的互补可行解，那么 $\mathbf{P}$ 和 $(\mathbf{f}, \mathbf{g})$ 同时是原问题和对偶问题的最优解。

(Proof)

4.Vertices of the Transportation Polytope

一个具有非空且有界可行域的线性规划在可行域的极点处取得其最小值 (单纯形法）。由于原始最优传输问题的可行域 $U(a, b)$ 是有界的，因此可以将最优 $\mathbf{P}$ 的搜索限制在多面体 $U(a, b)$ 的极点集合上。

4.1 Tree Structure of the Support of all Vertices of U(a, b)

设 $V = {1, 2, \ldots, n}$ 和 $V^\prime = {1^\prime, 2^\prime, \ldots, m^\prime}$ 为两个节点集。

• 并集 $V \cup V^\prime$，包含 $n+m$ 个节点，
• $\mathcal{E}：nm$ 条有向边的集合 $\{(i,j^{\prime}),i\in[[n]],j\in[[m]]\}$，对于每条边 $(i, j^\prime)$，关联权重 $\mathbf{C}_{ij}$
• $V$ 和 $V^\prime$ 之间的完全二分图 $\mathcal{G}$ 表示为 $(V \cup V^\prime, \mathcal{E})$。
  
  

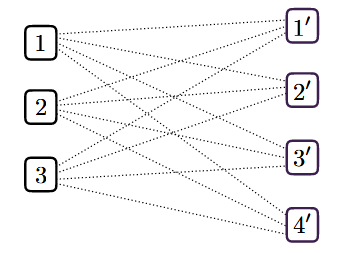
Transport plan 可以看作是图上的一个”flow“，它满足源约束（每个节点 $i$ 流出的量为 $\mathbf{a}_i$）和汇约束（每个节点 $j^\prime$ 流入的量为 $\mathbf{b}_j$）。

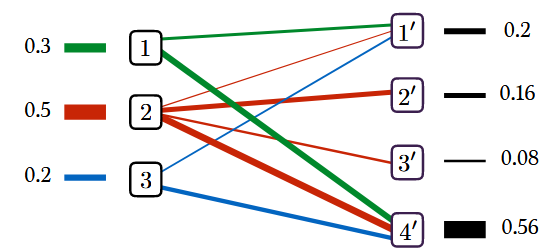
回顾$\mathbf{U}(\mathbf{a}, \mathbf{b})$的定义，其实际上是一个在约束条件(等式约束）下的矩阵集合，定义为：

$$
\mathbf{U}(\mathbf{a}, \mathbf{b}) \overset{\mathrm{def.}}{\operatorname*{=}} \left\{ \mathbf{P} \in \mathbb{R}_+^{n \times m} : \mathbf{P} \mathbb{1}_m = \mathbf{a} \quad \mathrm{and} \quad \mathbf{P}^\mathrm{T} \mathbb{1}_n = \mathbf{b} \right\}.
$$

这意味着 $\mathbf{U}(\mathbf{a}, \mathbf{b})$ 是一个由 传输约束 确定的多面体,其极点可以被看作该多面体的“顶点”, 这些极点对应特殊的传输矩阵, 有以下性质：

设 $\mathbf{P}$ 是多面体 $\mathbf{U}(\mathbf{a}, \mathbf{b})$ 的一个极点。令 $F(\mathbf{P}) \subset \mathcal{E}$ 为边集 $\{(i,j^{\prime}),i\in[n],j\in[m],s.t.P_{i,j}>0\}$
则图 $G(\mathbf{P}) \overset{\mathrm{def.}}{=} (V \cup V^\prime, F(\mathbf{P}))$ 中没有环。特别地，$\mathbf{P}$ 的非零元素数目不超过 $n + m - 1$

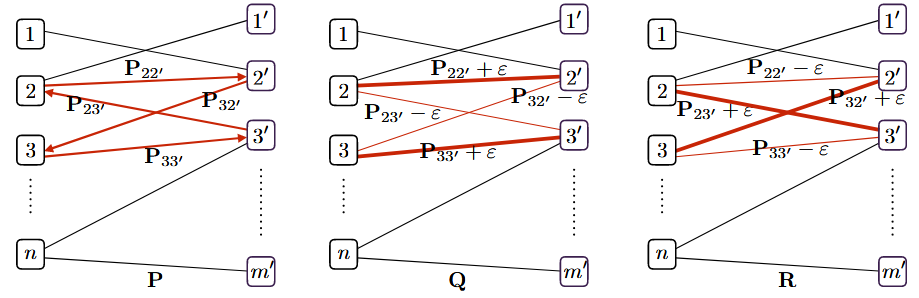
Proof:
设 $\mathbf{P}$ 是多面体 $\mathbf{U}(\mathbf{a}, \mathbf{b})$ 的一个极点。

反设其对应的边集 $F(\mathbf{P})$ 使得图 $G = (V \cup V^\prime, F)$ 包含一个环。即，存在 $k > 1$ 和一组不同的索引 $i_1, \ldots, i_k \in [n]$ 以及 $j_1, \ldots, j_k \in [m]$，使得边集 $H = {(i_1, j_1^\prime), (i_2, j_1^\prime), (i_2, j_2^\prime), \ldots, (i_k, j_k^\prime), (i_1, j_k^\prime)}$ 是 $F$ 的一个子集

为了构造反证，定义一个与 $H$ 对应的有向环 $\bar{H}$，其包含的路径为：

$$
i_1 \to j_1^\prime, j_1^\prime \to i_2, i_2 \to j_2^\prime, \ldots, i_k \to j_k^\prime, j_k^\prime \to i_1.
$$

我们定义一个扰动矩阵 $E$，它的 $(i, j)$ 项如下：

• 如果 $(i \to j^\prime) \in \bar{H}$，则 $E_{ij} = \varepsilon$；
• 如果 $(j^\prime \to i) \in \bar{H}$，则 $E_{ij} = -\varepsilon$；
• 否则，$E_{ij} = 0$

其中，$\varepsilon$ 是一个小于 $\min_{(i,j^\prime) \in F} \mathbf{P}_{ij}$ 的正数

接着基于矩阵 $E$，定义： $\mathbf{Q} = \mathbf{P} + E, \quad \mathbf{R} = \mathbf{P} - E$

不难验证 $\mathbf{Q}$ 和 $\mathbf{R}$ 满足：非负性 且 $\mathbf{Q}$ 和 $\mathbf{R}$ 的边缘分布与 $\mathbf{P}$ 相同

如此得到P的一个分解式：$\mathbf{P} = (\mathbf{Q} + \mathbf{R}) / 2$，且 $\mathbf{Q} \neq \mathbf{P}$，$\mathbf{R} \neq \mathbf{P}$。因此，$\mathbf{P}$ 被分解为两个不同矩阵的凸组合，这与 $\mathbf{P}$ 是极端点的假设相矛盾

进一步的可以得出$G$ 必须是无环的。而无环图的性质（PS：图论，这个了解不多）表明，$G$ 中的边数不能超过节点数减一，即 $n + m - 1$。因此，$\mathbf{P}$ 中非零元素的个数（即 $F(\mathbf{P})$ 中的边数）也不能超过 $n + m - 1$

4.2 The North-West Corner Rule

The North-West Corner Rule 是一种启发式方法，最多通过 $n + m$ 次操作生成多面体 $\mathbf{U}(\mathbf{a}, \mathbf{b})$ 的一个极点。这个启发式方法可以用来初始化任何在原始问题上工作的算法，例如下一节中提到的网络单纯形算法。

算法如下工作：

• 初始化 $i$ 和 $j$ 为 $1$，$r \leftarrow \mathbf{a}_1$，$c \leftarrow \mathbf{b}_1$。
• 在 $i \leq n$ 且 $j \leq m$ 时，设置 $t \leftarrow \min(r, c)$，然后 $\mathbf{P}_{i,j} \leftarrow t$，更新 $r \leftarrow r - t$，$c \leftarrow c - t$；
• 如果 $r = 0$，则增大 $i$，并在 $i \leq n$ 时更新 $r \leftarrow \mathbf{a}_i$；
• 如果 $c = 0$，则增大 $j$，并在 $j \leq m$ 时更新 $c \leftarrow \mathbf{b}_j$；
• 重复上述步骤。

例如，对a = [0.2, 0.5, 0.3]，b = [0.5, 0.1, 0.4]

$$
\begin{aligned}
\begin{bmatrix}
\bullet & 0 & 0 \\0 & 0 & 0 \\0 & 0 & 0\end{bmatrix}
&\to
\begin{bmatrix}0.2 & 0 & 0 \\\bullet & 0 & 0 \\0 & 0 & 0\end{bmatrix}
\to
\begin{bmatrix}0.2 & 0 & 0 \\0.3 & \bullet & 0 \\0 & 0 & 0\end{bmatrix} \\ & \to
\begin{bmatrix}0.2 & 0 & 0 \\0.3 & 0.1 & \bullet \\0 & 0 & 0\end{bmatrix}
\to
\begin{bmatrix}0.2 & 0 & 0 \\0.3 & 0.1 & 0.1 \\0 & 0 & \bullet
\end{bmatrix}
\to
\begin{bmatrix}0.2 & 0 & 0 \\0.3 & 0.1 & 0.1 \\0 & 0 & 0.3\end{bmatrix}
\end{aligned}$$

称通过上述算法得到的矩阵为$NW(a,b)$。 可通过任意排列 $a$ 和 $b$ 的顺序，首先计算对应的NW矩阵，然后通过再次反转行和列的顺序来恢复，得到 $\mathcal{N}(\mathbf{a}, \mathbf{b})$：

$$
\mathcal{N}(\mathbf{a}, \mathbf{b}) \overset{\mathrm{def.}}{=} \{ \mathbf{NW}_{\sigma^{-1}\sigma^{\prime-1}}(r_\sigma, c_{\sigma^{\prime}}), \sigma, \sigma^{\prime} \in S_d \}.
$$

5.A Heuristic Description of the Network Simplex

5.1 Obtaining a Dual Pair Complementary to P

单纯形法首先将任意极点$\mathbf{P}$ 与一对互补的对偶变量 $(\mathbf{f}, \mathbf{g})$ 相关联, 需要找到两个向量 $\mathbf{f} 和 \mathbf{g}$，使得对于 $F(\mathbf{P})$中的任意$(i, j^\prime)$，有 $\mathbf{f}_i + \mathbf{g}_j = \mathbf{C}_{i,j}$。

令 s 为 $F(P)$ 的基数。由于 $\mathbf{P}$ 是极点，因此 $s \leq n + m - 1$。由于 $G(\mathbf{P})$ 无环，因此它是一个树或一个森林。

为了找到与 $\mathbf{P}$ 互补的一对$(\mathbf{f}, \mathbf{g})$，我们考虑对 $n + m$ 个变量施加如下s个线性等式约束：

$$\begin{aligned} &\mathbf{f}_{i_1} + \mathbf{g}_{j_1} = \mathbf{C}_{i_1,j_1} \\ &\mathbf{f}_{i_2} + \mathbf{g}_{j_1} = \mathbf{C}_{i_2,j_1} \\ &\vdots \\ &\mathbf{f}_{i_s} + \mathbf{g}_{j_s} = \mathbf{C}_{i_s,j_s}, \end{aligned}$$

例如，在下图中，有$5 + 6 = 11$个对偶变量，但这 11 个节点之间只有 8 条边，因此仅定义了 8 个线性方程。

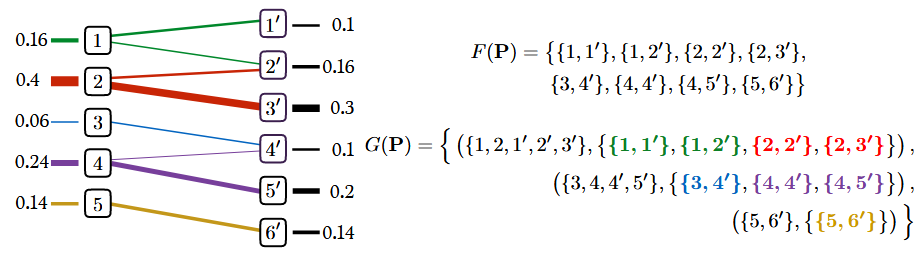
考虑 $G(\mathbf{P})$ 中的某棵树。假设这棵树中有 k 个源节点，分别是$i1,…,iki_1, \ldots, i_k$以及 l 个目标节点，分别是 $j1′,…,jl′j_1^\prime, \ldots, j_l^\prime$。节点总数为$r = k + l$，这棵树包含$r−1$条边，则对应于 $f$ 中的 $k$个变量和 $\mathbf{g}$ 中的$l$个变量，由 r−1个线性方程联系起来。

为了解除一个自由度的不确定性，可以在这棵树中任意选择一个根节点（root node），并将与该节点对应的对偶变量赋值为 0。从这个根节点出发，可以使用广度优先搜索（BFS）或深度优先搜索（DFS）遍历整棵树，通过简单的变量赋值序列确定树中所有其他对偶变量的值。这一过程可以对$G(\mathbf{P})$ 中的所有树重复进行，从而得到一对与$\mathbf{P}$ 互补的对偶变量$(\mathbf{f}, \mathbf{g})$

与前面图相对应，$G(\mathbf{P})$ 的第一棵树的 5 个节点对应的 5 个对偶变量 $f_1, f_2, g_1, g_2, g_3$，通过 4 个线性方程与成本矩阵 $\mathbf{C}$ 中的相应条目相关联。由于该线性系统是欠定的，我们可以选择该树中的一个节点作为根节点（例如节点 1），并将其对应的对偶变量设为 0。接着，从根节点出发，使用广度优先或深度优先的方式遍历整棵树，逐步迭代计算其余 4 个对偶变量的值。

5.2 Network Simplex Update

之前得到的对偶对 $(\mathbf{f}, \mathbf{g})$ 可能是可行的，即对于所有$i, j$，都有$\mathbf{f}_i + \mathbf{g}_j \leq \mathbf{C}_{i,j}$。在这种情况下，由对偶理论，我们已经达到了最优解。

然而，如果存在$i,j$ 满足$\mathbf{f}_i + \mathbf{g}_j > \mathbf{C}_{i,j}$，考虑用网络单纯形算法更新。

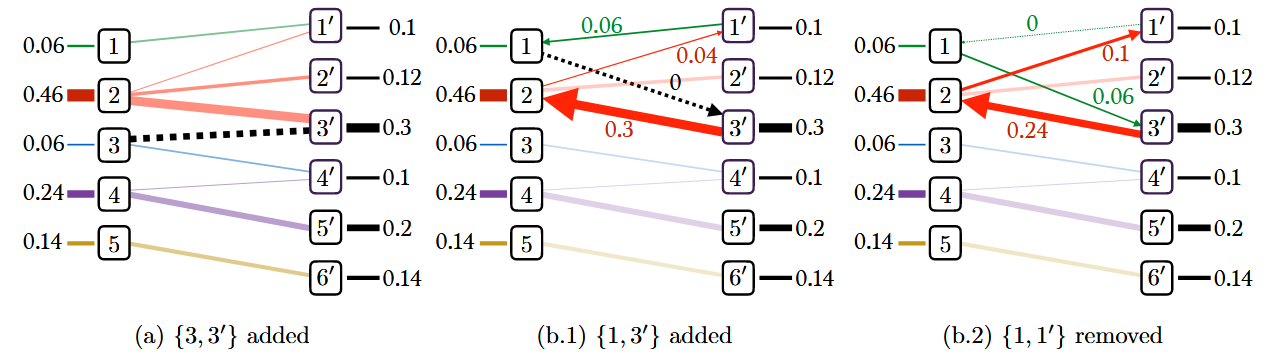
首先，初始化一个图 $G$，令其等于与可行解 $\mathbf{P}$ 对应的图 $G(\mathbf{P})$，并将违反约束的边$(i, j^\prime)$添加到 GG。随后会出现两种情况：

1. $G$ 仍然是森林
   这可能发生在$(i, j^\prime)$ 连接了两个现有子树时。仍使用 5.1 节中描述的方法，在图 $G$ 上恢复一个新的互补对偶向量 $(\mathbf{f}, \mathbf{g})$。
   • 此操作仅消除了$n+m$ 个对偶变量中的一个不确定性，并不会改变原始变量 $\mathbf{P}$。
   • 这种更新被称为“退化更新”（degenerate update），因为虽然$(i, j^\prime)$ 已加入图 $G$，但 $\mathbf{P}_{i,j}$ 仍然保持为 0，同时$G(\mathbf{P})$ 是 $G$ 的一个子集。
2. $G$ 出现了一个环
   如果 $G$ 中出现了环$\begin{aligned}(i_1,j_1'),(j_1',i_2),(i_2,j_2'),\ldots,(i_l,j_l'),(j_l',i_{l+1})\end{aligned}$，其中$i_1= i_{l+1}$。需要从 $G$ 中移除一条边以保持 $G$ 是森林，同时修改 $\mathbf{P}$，以确保 $\mathbf{P}$可行且 $G(\mathbf{P})$仍然包含在 $G$ 中。这可以通过以下步骤完成：
   • 增加边$(i_k, j_k^\prime)$ ，$k <= l$上的流量，同时减少环中另一方向上的流量（即 $(j_k^\prime, i_{k+1}$)。
   • 这将产生一个更新的原始解 $\tilde{\mathbf{P}}$，其中：$$ \tilde{\mathbf{P}}_{i_k, j_k} = \mathbf{P}_{i_k, j_k} + \theta, \quad \tilde{\mathbf{P}}_{i_{k+1}, j_k} = \mathbf{P}_{i_{k+1}, j_k} - \theta $$
     $\theta$ 是可以增加的最大值，其值由环中受负面影响的最小流量控制，即 $\theta = \min_k \mathbf{P}_{i_{k+1}, j_k}$。
   • 找到最小值的索引 $k^\star$，并从 $G$ 中移除边$(i_{k^\star+1}, j_{k^\star})$。随后，使用 5.1 节的方法计算新的对偶变量$(\mathbf{f}, \mathbf{g})$。
     
     

网络单纯形算法可以总结如下：

• 初始化： 使用一个极值解 $\mathbf{P}$ 初始化算法（e.g. North-West Corner Rule））。初始化图 $G$ 为 $G(\mathbf{P})$
• 计算对偶变量： 计算一对对偶变量 $(\mathbf{f}, \mathbf{g})$，使其与 $\mathbf{P}$ 互补，使用线性系统求解并利用图 $G$ 中的树结构进行
• 检查约束：
  (i) 查找违反约束$\mathbf{C} - \mathbf{f} \oplus \mathbf{g} \geq 0$ 的索引对。如果没有违反的对，则说明 $\mathbf{P}$ 已经是最优解，停止
  (ii) 如果存在违反约束的索引对 $(i, j')$，
  (iii) 将边 $(i, j')$ 添加到图 $G$
• 图的更新：
  (i)如果图 $G$仍然没有形成环，则根据情况更新对偶变量$(\mathbf{f}, \mathbf{g})$；
  (ii)如果图 (G 形成了环，则将环进行定向，确保$(i, j')$ 被标记为正边，并移除该环中流量值最小的负边，同时更新 $\mathbf{P}$ 和 $G$。然后根据新的更新，重新计算对偶变量 $\mathbf{f} 和 \mathbf{g}$.
• 重复操作：
  重复上述操作，直到满足最优条件。

6. Dual Ascent Methods

欠着

7. Auction Algorithm

欠着