参考自：第 10 章 搜索

1.二分查找

 二分查找（binary search）是一种基于分治策略的高效搜索算法。它利用数据的有序性，每轮缩小一半搜索范围，直至找到目标元素或搜索区间为空为止。

Question：
给定一个长度为 n 的数组 nums ，元素按从小到大的顺序排列且不重复。请查找并返回元素 target 在该数组中的索引。若数组不包含该元素，则返回 −1 。

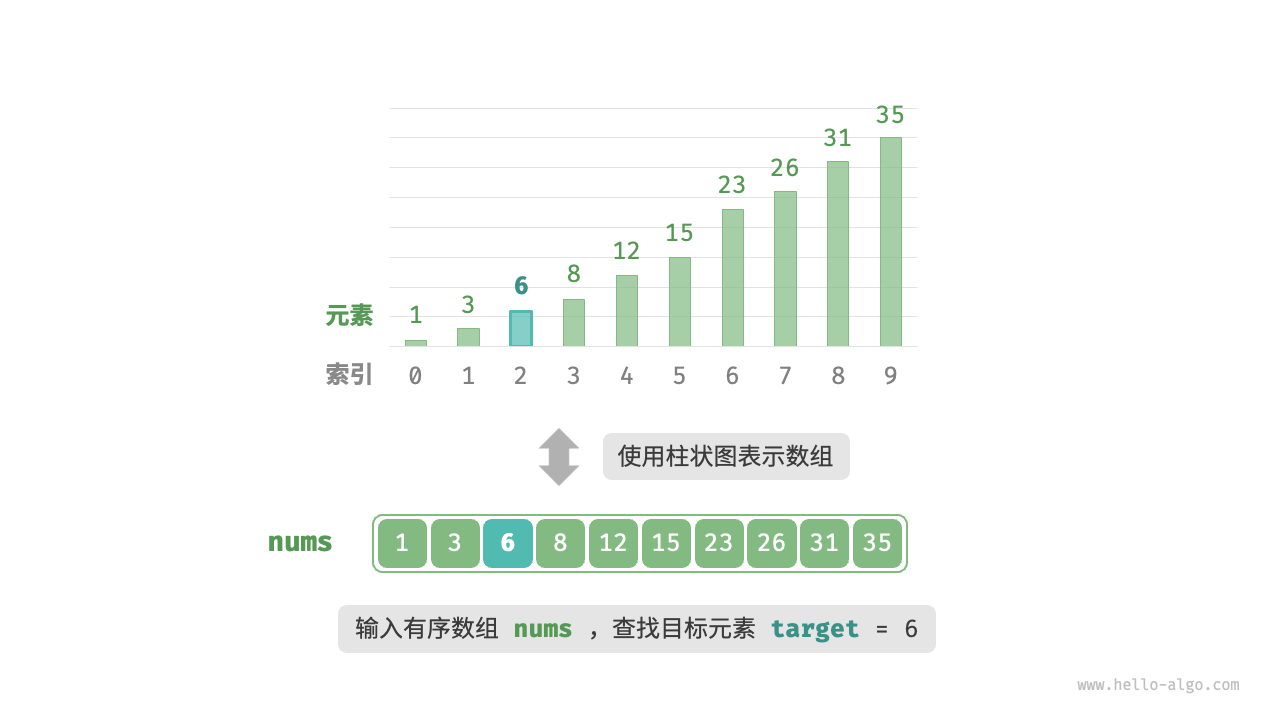
初始化指针$i=0$和$j=n-1$ ,分别指向数组首元素和尾元素，代表搜索区间$[0,n-1]$。
循环执行:

1. 计算中点索引 $m=\lfloor(i+j)/2\rfloor$ , （向下取整）。
2. 判断 nums[m] 和 target 的大小关系:
   a.当 nums[m]< target 时，说明 target 在区间$[m+1,j]$中，因此执行$i=m+1$ 
   b.当 nums[m]> target 时，说明 target 在区间$[i,m-1]$中，因此执行$j=m-1$ 
   c.当 nums[m]= target 时，说明找到 target,因此返回索引$m$

PS:

• 若数组不包含目标元素，搜索区间最终会缩小为空。此时返回-1 。
• 为了避免大数越界，我们通常采用公式$m=|i+(j-i)/2|$来计算中点 (python不用担心)
• 时间复杂度：$O(log n)$
• 空间复杂度：$O(1)$

def binary_search(nums: list[int], target: int):
    """二分查找"""
    # 初始化区间 [0, n-1]
    i, j = 0, len(nums) - 1
    
    while i <= j:
        m = (i + j) // 2  # 中点索引 m
        if nums[m] < target:
            i = m + 1  #  target 位于 [m+1, j] 
        elif nums[m] > target:
            j = m - 1  #  target 位于 [i, m-1] 
        else:
            return m   # 找到目标元素
    return -1  # 未找到目标元素，返回 -1

二分查找并非适用于所有情况：

• 二分查找仅适用于有序数据。若输入数据无序，为了使用二分查找而专门进行排序，但排序算法的时间复杂度通常为 $O(nlog⁡n)$ ，比线性查找和二分查找都更高。
• 二分查找仅适用于数组。二分查找需要跳跃式（非连续地）访问元素，而在链表中执行跳跃式访问的效率较低，因此不适合应用在链表或基于链表实现的数据结构。
• 小数据量下，线性查找性能更佳。在线性查找中，每轮只需 1 次判断操作；而在二分查找中，需要 1 次加法、1 次除法、1 ~ 3 次判断操作、1 次加法（减法），共 4 ~ 6 个单元操作。

2.二分查找插入点

 二分查找不仅可用于搜索目标元素，还可用于解决许多变种问题，比如搜索目标元素的插入位置。

2.1 无重复元素的情况

[!question] Question
给定一个长度为 n 的有序数组 nums 和一个元素 target ，数组不存在重复元素。现将 target 插入数组 nums 中，并保持其有序性。若数组中已存在元素 target ，则插入到其左方。请返回插入后 target 在数组中的索引。

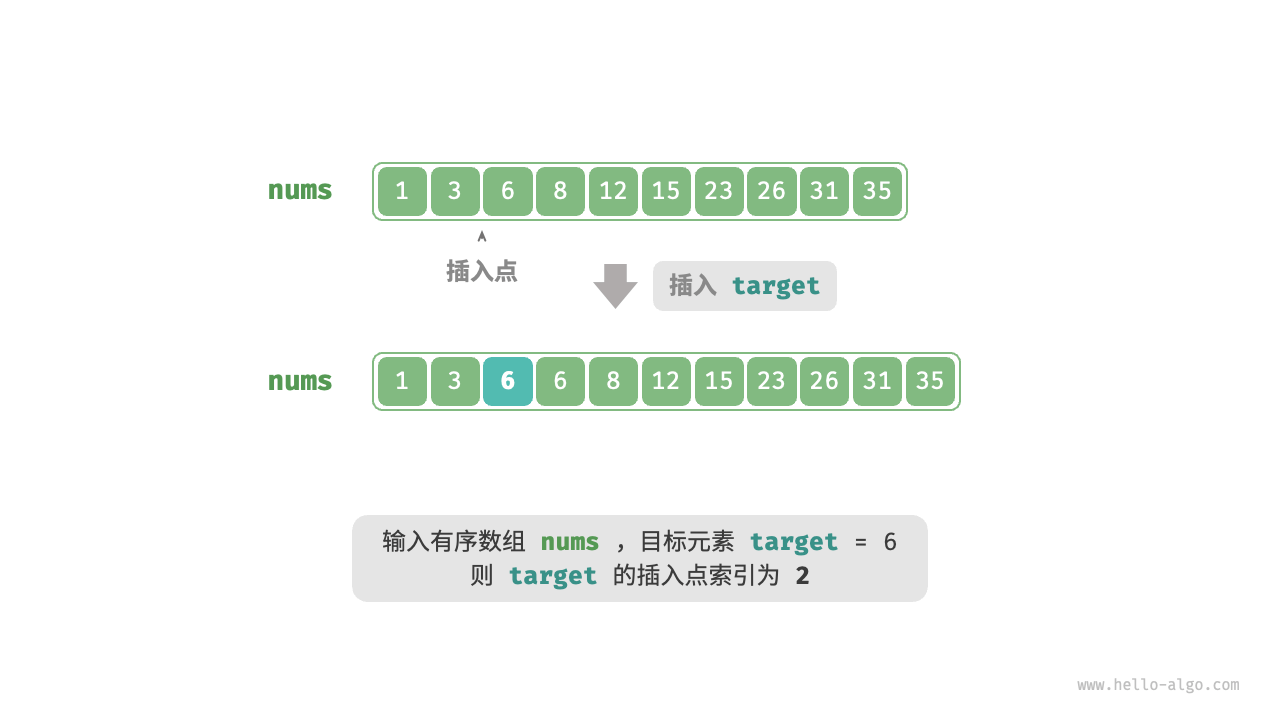
def binary_search_insertion_simple(nums: list[int], target: int):
    """二分查找插入点（无重复元素）"""
    i, j = 0, len(nums) - 1 
    while i <= j:
        m = (i + j) // 2
        if nums[m] < target:
            i = m + 1
        elif nums[m] > target:
            j = m - 1 
        else:
            return m 
    # 未找到 target ，返回插入点 i
    return i

这里有几个注意的点。首先，题目要求若数组中已存在元素target，则插入到其左方，注意到上述代码关于中点的选择为向下取整，所以当判断索引处值为targe时，可直接返回。其次，注意到当循环退出时，i 指向首个大于 target 的元素，j 指向首个小于 target 的元素, 所以此时返回索引i。

2.2 存在重复元素的情况

[!question] Question
在上一题的基础上，规定数组可能包含重复元素，其余不变。

 假设数组中存在多个 target ，题目要求将目标元素插入到最左边，所以我们需要查找数组中最左一个 target 的索引

 拓展二分查找代码。整体流程保持不变，唯一改变的是：

• 当 nums[m] == target 时，说明小于 target 的元素在区间 [i,m−1] 中，因此采用 j=m−1 来缩小区间，从而使指针 j 向小于 target 的元素靠近。

 循环完成后，i 指向最左边的 target ，j 指向首个小于 target 的元素，因此索引 i 就是插入点。

def binary_search_insertion(nums: list[int], target: int):
    """二分查找插入点（存在重复元素）"""
    i, j = 0, len(nums) - 1 
    while i <= j:
        m = (i + j) // 2 
        if nums[m] < target:
            i = m + 1 
        elif nums[m] > target:
            j = m - 1 
        else:
            j = m - 1  # 首个小于 target 的元素在区间 [i, m-1] 中
    return i

3. 二分查找边界

3.1 查找左边界

Question：
给定一个长度为 n 的有序数组 nums ，其中可能包含重复元素。请返回数组中最左一个元素 target 的索引。若数组中不包含该元素，则返回 −1 。

与上题类似，注意，当数组中不包含 target 时可能导致以下两种结果。

• 插入点的索引 i 越界。
• 元素 nums[i] 与 target 不相等。

def binary_search_left_edge(nums: list[int], target: int):
    """二分查找最左一个 target"""
    i = binary_search_insertion(nums, target)
    
    # 未找到 target ，返回 -1
    if i == len(nums) or nums[i] != target:
        return -1

    return i

3.2 查找右边界

3.2.1 复用查找左边界

实际上，我们可以利用查找最左元素的函数来查找最右元素，具体方法为：将查找最右一个 target 转化为查找最左一个 target + 1。
查找完成后，指针 i 指向最左一个 target + 1（如果存在），而 j 指向最右一个 target ，因此返回 j 即可。

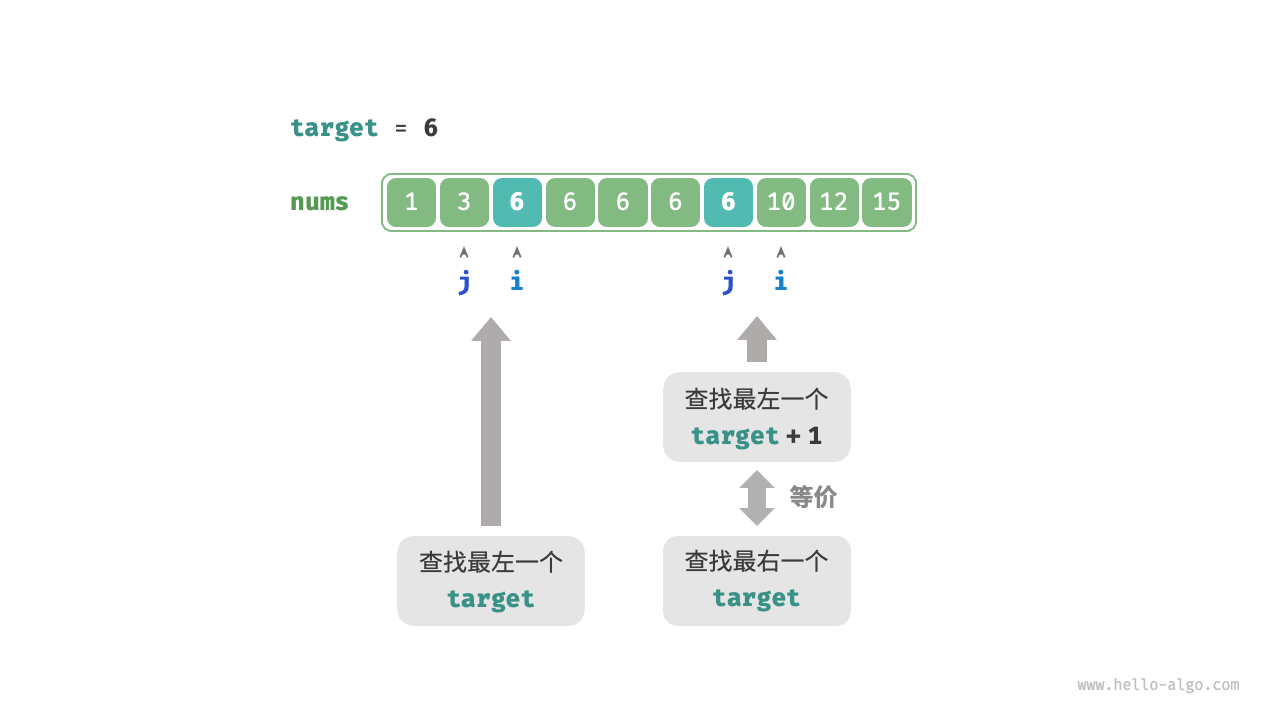
请注意，返回的插入点是 i ，因此需要将其减 1 ，从而获得 j ：

def binary_search_right_edge(nums: list[int], target: int) -> int:
    """二分查找最右一个 target"""
    # 转化为查找最左一个 target + 1
    i = binary_search_insertion(nums, target + 1)
    # j 指向最右一个 target ，i 指向首个大于 target 的元素
    j = i - 1
    # 未找到 target ，返回 -1
    if j == -1 or nums[j] != target:
        return -1
    # 找到 target ，返回索引 j
    return j

3.2.2   转化为查找元素¶

当数组不包含 target 时，最终 i 和 j 会分别指向首个大于、小于 target 的元素。
因此，可以构造一个数组中不存在的元素，用于查找左右边界。

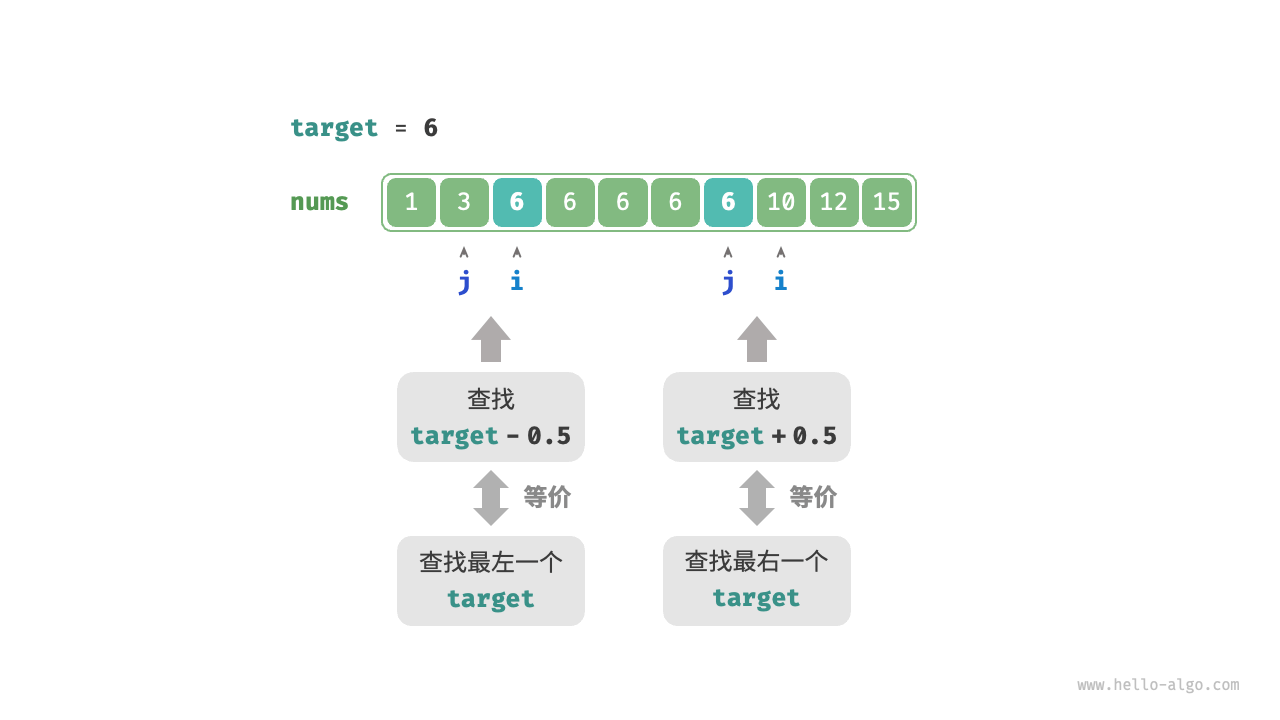
• 查找最左一个 target ：可以转化为查找 target - 0.5 ，并返回指针 i 。
• 查找最右一个 target ：可以转化为查找 target + 0.5 ，并返回指针 j 。
• 给定数组不包含小数，这意味着我们无须关心如何处理相等的情况。

4. 哈希优化策略

Question：
给定一个整数数组 nums 和一个目标元素 target ，请在数组中搜索“和”为 target 的两个元素，并返回它们的数组索引。返回任意一个解即可。

4.1   线性查找

 考虑直接遍历所有可能的组合。使用二层循环，在每轮中判断两个整数的和是否为 target ，若是，则返回它们的索引。
此方法的时间复杂度为 $O(n^2)$ ，空间复杂度为 $O(1)$ ，在大数据量下非常耗时。

10.4.2   哈希查找：以空间换时间

考虑借助一个哈希表，键值对分别为数组元素和元素索引。循环遍历数组，每轮执行：

1. 判断数字 target - nums[i] 是否在哈希表中，若是，则直接返回这两个元素的索引。
2. 将键值对 nums[i] 和索引 i 添加进哈希表。

def two_sum_hash_table(nums: list[int], target: int):
    """辅助哈希表"""
    dic = {}

    for i in range(len(nums)):
        if target - nums[i] in dic:
            return [dic[target - nums[i]], i]
        dic[nums[i]] = i
        
    return []

 此方法通过哈希查找将时间复杂度从 $O(n^2)$ 降至 $O(n)$ ，大幅提升运行效率。
由于需要维护一个额外的哈希表，因此空间复杂度为 $O(n)$ 。

5. 搜索算法

 搜索算法（searching algorithm）用于在数据结构（例如数组、链表、树或图）中搜索一个或一组满足特定条件的元素。

 搜索算法可根据实现思路分为以下两类。

• 通过遍历数据结构来定位目标元素，例如数组、链表、树和图的遍历等。
• 利用数据组织结构或数据包含的先验信息，实现高效元素查找，例如二分查找、哈希查找和二叉搜索树查找等。

5.1   暴力搜索

暴力搜索通过遍历数据结构的每个元素来定位目标元素。

• “线性搜索”适用于数组和链表等线性数据结构。它从数据结构的一端开始，逐个访问元素，直到找到目标元素或到达另一端仍没有找到目标元素为止。
• “广度优先搜索”和“深度优先搜索”是图和树的两种遍历策略。广度优先搜索从初始节点开始逐层搜索，由近及远地访问各个节点。深度优先搜索从初始节点开始，沿着一条路径走到头，再回溯并尝试其他路径，直到遍历完整个数据结构。

 暴力搜索的优点是简单且通用性好，无须对数据做预处理和借助额外的数据结构。然而，此类算法的时间复杂度为 O(n) ,因此在数据量较大的情况下性能较差。

5.2   自适应搜索

 自适应搜索利用数据的特有属性（例如有序性）来优化搜索过程，从而更高效地定位目标元素。

• “二分查找”利用数据的有序性实现高效查找，仅适用于数组。
• “哈希查找”利用哈希表将搜索数据和目标数据建立为键值对映射，从而实现查询操作。
• “树查找”在特定的树结构（例如二叉搜索树）中，基于比较节点值来快速排除节点，从而定位目标元素。

 此类算法的优点是效率高，时间复杂度可达到 O(log⁡n) 甚至 O(1) 。

 然而，使用这些算法往往需要对数据进行预处理。例如，二分查找需要预先对数组进行排序，哈希查找和树查找都需要借助额外的数据结构，维护这些数据结构也需要额外的时间和空间开销。

5.3   搜索方法选取

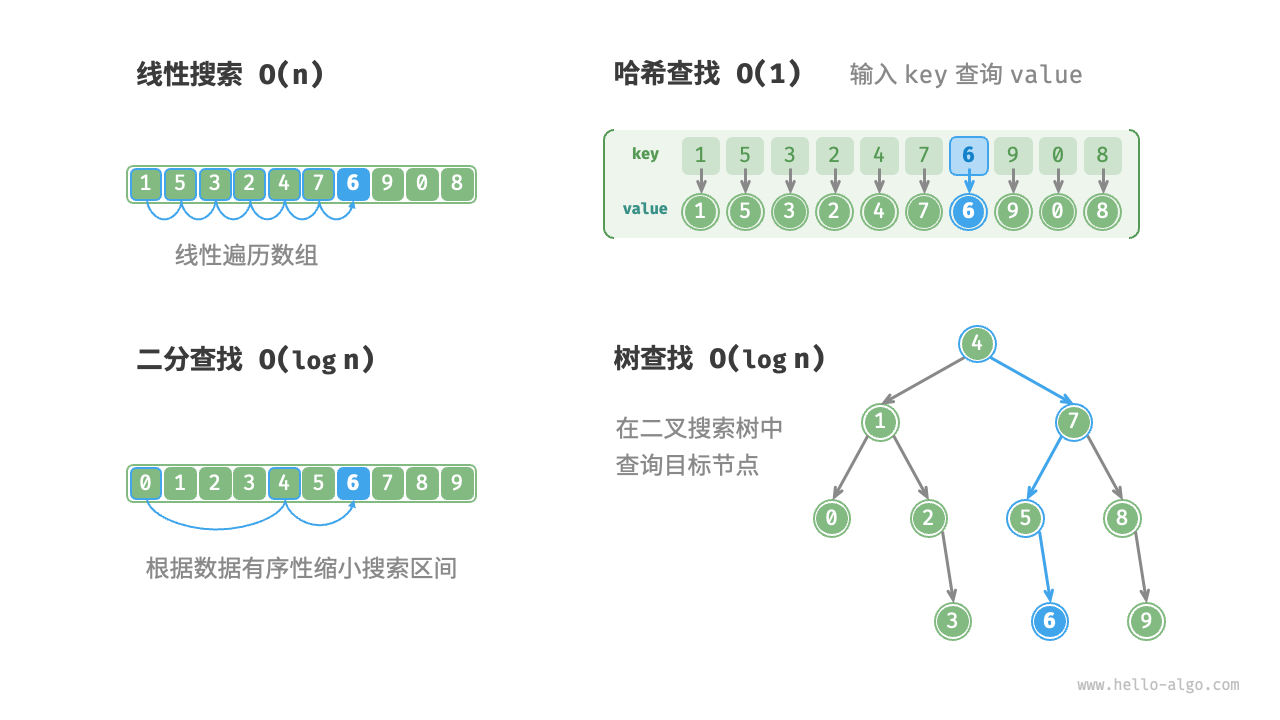
 给定大小为 n 的一组数据，我们可以使用线性搜索、二分查找、树查找、哈希查找等多种方法从中搜索目标元素。

	线性搜索	二分查找	树查找	哈希查找
查找元素	O(n)	O(log⁡n)	O(log⁡n)	O(1)
插入元素	O(1)	O(n)	O(log⁡n)	O(1)
删除元素	O(n)	O(n)	O(log⁡n)	O(1)
额外空间	O(1)	O(1)	O(n)	O(n)
数据预处理	/	排序 O(nlog⁡n)	建树 O(nlog⁡n)	建哈希表 O(n)
数据是否有序	无序	有序	有序	无序